Statistics of Human Average Penis Size
The size of the human penis is something that concerns all men. It is often seen as being a manifestation of one's manhood, and as such most men are interested in knowing how their own size compares to others. The average penis length is usually reported to be about 14 cm, or about 5.5 inches.
However, it is likely that this value is an underestimate. Since having a large penis size is so important, it is beneficial to both small and large men to deflate the average size. For small men, this helps one to feel more "normal", or to ease the internalized humiliation one can feel at being less than other men. For average or larger men, reducing the reported average has the benefit of making one feel more confident about one's size.
This study seeks to establish an estimate of the average human penis size based on self-reported data. We will attempt to remove any biases evident in the data and establish where the true mean lies, what the distribution of sizes is, and offer some suggestions about where qualitative terms like "small", "average", "large", and "hung" should come into use.
We will be examining data from the our website for which users measure their own penises and enter both their length and girth, in centimetres, into the system when registering. The purpose of the site is to allow members to compare their penis sizes to establish who is bigger (by volume), either winning or losing "manhood" points in the process.
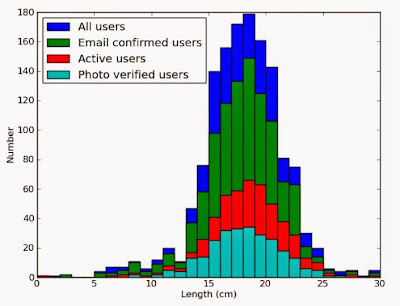
While one could easily overstate their actual size, it is thought that by doing so one takes the fun out of subsequent bets and comparison. Nonetheless, there are some additional protections in place to ensure accurate sizes. Before one can make any comparisons, one must confirm their email address, and upload a "bulge pic", which is a photo of their penis in underwear, swimwear, or similar, to give a suggestion of the actual size without giving away the exact number. This bulge pic is the only information uses have when sizing each other up before betting manhood on a comparison. The final step is to upload a "verification" pic, which includes a photo of one's username next to their penis, so that the site administrator has proof that the photos belong to the user in control of the account. Many users who upload verification pics will also upload pictures of their penis being measured, according to specific instructions on the site. Whenever photos show a different size than reported, or show evidence of being doctored to appear larger, the site administrator can either deduct manhood from the user or adjust their reported size manually. Histograms of length and girth can be seen in Figures 1 and 2 respectively. Note that with each additional verification step completed, the number of users drops (see Table 1).
We consider this data to represent a cross section of the general population, with some caveats. One natural bias in the userbase would be that a site such as CSC will select for men that are confident enough about their size to take part in comparisons with other men.
Figure 1: Histogram of penis length, in centimetres, with 1 cm width bins. Odd features, such as an excess at 8-9 cm, are diminished with each verification level. The overall distribution remains roughly constant, suggesting that there is not a strong correlation between size and verification. The total range of verified lengths is 8-27 cm (approxiately 3-11 inches).
Figure 2: Histogram of penis girth (i.e., circumference of the shaft), with 1 cm width bins. Similar to length, odd features diminish with each verification level. The total range in verified girth is 8-20 cm (approximately 3-8 inches). The equivalent range in diameters is 1-2.5 inches.
We will discuss whether this is a likely effect further in the next section, though for now one can already note that the distribution is nearly symetric, and that the peak remains constant as a function of verification level. As such, it is unlikely that we are missing a significant proportion of small men, nor is there any correlation with how much effort a man is willing to put into being verified on a site such as CSC and the mean size.
There are, however, some features of the distribution which merit additional attention. In particular, both length and girth show bumps at small numbers. The most likely explanation for these is that users are incorrectly entering their size in inches rather than centimetres. For length, the excess is at between 8 to 9 cm, which would be an impressive length if in inches. The bump in girth is much more substantial around 5 to 7 cm, which would correspond to a diameter of less than an inch, which possible though unlikely.
Based only on values reported at registration, it would be reasonable to exclude any lengths less than 9 cm and any girths less than 7 cm as being due to user error. However, it is noticeable that both these excesses disappear when the users are verified. It seems that these mistakes are weeded out naturally. Similarly, extremely large sizes are less likely to be verified, which suggests that these are men who were exaggerating their size and are unwilling to continue in that lie.
Based on this evidence, instead of applying arbitrary cuts on the data, we will consider the "photo verified" subset to be accurate, and will be used in all further analysis unless otherwise noted. Comparisons made between the verified subset and the larger sets can be used to estimate the effect of biases in self-reported data.
The null hypothesis is that penis size follows a normal (gaussian) distribution. Tables 1 and 2 lists the number of measurements for each the dataset and various simple statistics for length and girth, respectively. With increasing verification, mean length does not show a significant trend, while mean girth rises, suggesting that girth is typically underestimated. The median of both measures is constant, while the standard deviation decreases for both, suggesting that increased verification eliminates outliers on both ends of the distribution.
Also shown in these tables are the the best-fit gaussian parameters for the distribution. This fit is the best approximation of the actual mean xo and standard deviation σ from which these measurements are drawn. Both parameters are constant with verification level, within error, reinforcing the conclusion that there is not a significant bias in selecting men who are willing to be active members of a site such as CSC. It is interesting that xo and σ are not equal to the mean and standard deviation of the entire dataset, suggesting that the distribution is either not truly gaussian or at least still contains outliers. Figures 3 and 4 show these fits for the photo verified subsets of length and girth respectively.
Figure 3: Best-fit normal gaussian distribution for length of photo verified users.
Figure 4: Best-fit of normal gaussian distribution for girth of photo verified users.
There are a couple oddities which remain in the photo verified data which merrit some discussion. One of these is a deficit compared to the expected value from the gaussian fit in length in the 12 cm bin, which can be seen in Figure 3. This is likely due to the fact that 13 cm, the beginning of the next bin, is equal to about 5 inches. It seems that men who measure 12 or 12.5 cm (just under 5 inches) tend to want to over estimate their own size such that they do not have to suffer the humiliation of having a 4 inch penis. The gaussian fit to girth, seen in Figure 4, is not as good, but other than dificulty in measuring girth, there is not an obvious explanation for any of the features seen.
Table 3: Shapiro test results for the null hypothesis.
Given the above discussion, we should try to test the hypothesis that the length and girth follow a normal distribution more directly. To do so, we conduct the Shapiro-Wilk test. The results are shown in Table 3. The statistic W measures the likelihood that the data comes from a normal distribution. The ρ-value indicates the signifcance of the result. For all data subsets, W is close to one, though for all but the photo verified subset the ρ-value is very small (ι0.05), so these results are not considered significant. The low significance is likely due to incorrect measurements and other outliers discussed previously. However, for the photo verified subset, the ρ = 0.30, indicating that the null hypothesis can not be rejected. The Anderson-Darling test, not shown here, also indicated that only the photo verified dataset was likely to come from a true normal distribution.
We have shown that the length and girth data from photo verified CSC users follows a normal (gaussian) distribution. Lesser levels of verification exhibit features which are not consistent with a gaussian, but the basic statistics (including mean, standard deviation, and gaussian parameters) are not significantly biased by these features.
For this study, the only data from users used is their length and girth. No other information, such as race, height, weight, or age, is included. As such there may be additional correlations that are undetected here.
Using the gaussian fit as an indicator of the true underlying distribution of human penis size among adult men, we find the average length is 18.08±0.07 cm with a standard deviation of 2.16±0.05 cm. Similarly, the average girth is 14.37±0.08 cm with standard deviation of 1.42±0.06 cm. Based on this data, it seems evident that the average penis length commonly reported is indeed significantly understated. Approximately 68% of the population should fall within one standard deviation of the average (about 16-20 cm or 6.25-8 inches) and should be considered "normal". Those who are two standard deviations above this, i.e. greater than about 22 cm in length, comprise less than 3% of the population and certainly deserve the title "hung", while on the opposite end of the spectrum those less than 14 cm are equally rare and should be recognized as "small".
Unit conversion
As discussed, a common problem in measuring penis size is getting the units right. To convert from inches to centimeters, one must only multiply by 2.54. The conversion between girth and radius is
where G is the girth and R is the radius. To calculate volume, use
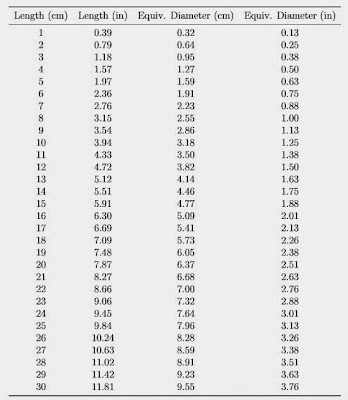
where V is volume and L is length. One must be careful to use the same units for all values. Table 4 lists the conversion between centimeters and inches, as well as the equivalent diameter assuming the given girth.
Table 4: The first two columns show the conversion between centimeters and inches. The last two columns show the diameter of the penis given the girth shown in the first column.







Comments
Post a Comment